| The apprehending zone is a model of student learning in social contexts. AZ informs implementation of constructivist philosophy in the form of objects, activities, and facilitation emphases. AZ foregrounds the complementarity of personal and interpersonal aspects of classroom learning processes. Student learning is interpreted as a personal multi-modal process of linking up situations and representations (see central bubble) as modeled by the teacher and peers in the classroom shared problem-solving space (arrows going in and out of the central bubble). Through this process, designed tools (bottom bubble) that initially have little if any meaning for the student are deployed in the spatial–temporal classroom space to be interwoven (linked, coordinated) into a concept-specific semiosis (central bubble). Thus, through participation in classroom activities the student has developed residual conceptual structures with sufficient overlap with those of the designer (top bubble), so as to be mathematically accurate enough. Abrahamson developed AZ as part of his dissertation project to investigate the evolution of proportional reasoning by monitoring a classroom’s discourse as they discuss mathematical stories and diagrams. This work led to a conviction that implicit dynamical embodied forms of reasoning and learning are under-theorized in the mathematics-education literature. |
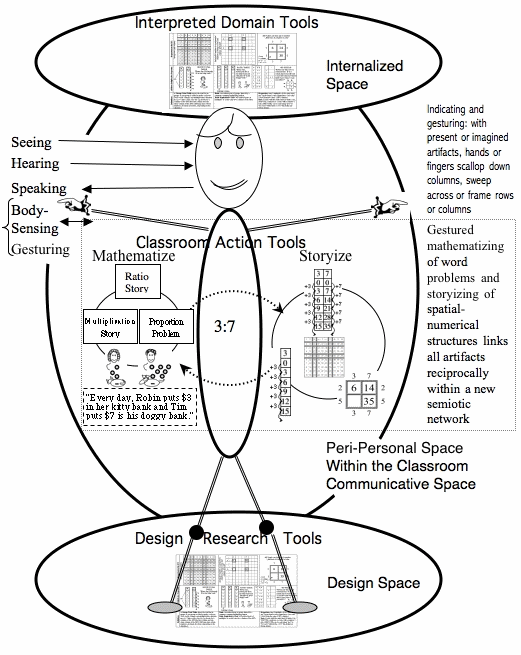
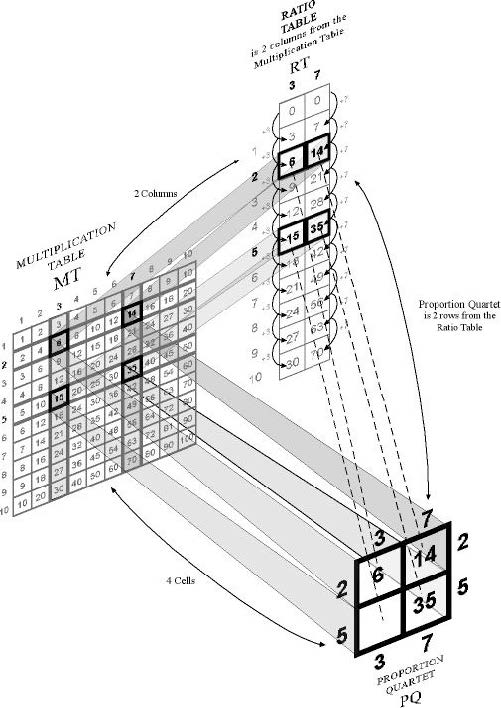
The dissertation was centered on a learning design for Grade 5 students to work with the familiar mulitiplication table so as to ground an understanding of proportional relations first as two linked repeated-addings in a ratio table and then as a muliptlicative structure. These designs are now part of a major curriculum.
The figure depicts mathematical formats in the ratio-and-proportion design space. In the experimental unit, students re-instrumentalize the multiplication table (MT) as a model of proportion situations. The ratio table (RT) is 2 columns embedded in and emanating out of the MT. The proportion quartet (PQ) is 4 products and their respective row/column-number factors embedded in and emanating from the MT or 2 rows from the RT.
Publications
Fuson, K. C., & Abrahamson, D. (2005). Understanding ratio and proportion as an example of the Apprehending Zone and Conceptual-Phase problem-solving models. In J. I. D. Campbell (Ed.), Handbook of mathematical cognition (pp. 213-234). New York: Psychology Press.OPENING: Learning mathematics requires learning to use culturally specific mathematical language, formats, and methods (math tools). To use these math tools effectively in a problem situation, one must learn to identify the mathematical elements of that problem situation; i.e., one must learn to mathematize . In traditional approaches to mathematics learning, these aspects are often separated, with problem solving following learning about mathematical tools. We present in this chapter a model for learning mathematics with understanding that highlights the kinds of connections that can facilitate sense-making by the learner. We exemplify this model with a new approach to the learning of ratio and proportion. This approach addresses two major learning difficulties in this domain (e.g., Behr, Harel, Post, & Lesh, 1993; Harel & Confrey, 1994; Kaput & West, 1994; Lamon, 1999). First, students typically use additive rather than multiplicative solution methods (e.g., to solve 6:14 = ?:35, they find the difference between 6 and 14 and subtract it from 35 to find 27:35 rather than seek multiplicative relationships). Second, they have difficulty moving from easy problems that use the basic ratio (e.g., 3:7 = ?:14) to middle-difficulty nondivisible problems in which neither ratio is a multiple of the other (e.g., 6:14 = ?:35).
Abrahamson, D. (2004). Keeping meaning in proportion: The multiplication table as a case of pedagogical bridging tools. Unpublished doctoral dissertation. Northwestern University, Evanston, IL. Accessed Dec 20, 2013 at ISBN 0-496-79720-0.
ABSTRACT: The broad agenda of this dissertation is the design of mathematics curricula for elementary and middle-school students to build meaning for and fluency with mathematical concepts. The paradigm of the work is design research, which combines empirical and theoretical studies. The empirical substance of this dissertation is a set of studies that were implementations of an experimental curricular unit for 5th-grade students learning the domain of ratio and proportion. The theoretical component of this paper is the apprehending zone (Fuson & Abrahamson, 2005), a Piagetian–Vygotskiian conceptual–practical model of design, teaching, and learning in mathematics classrooms. The design positions the multiplication table as the central representation for ratio and proportion. Students working with the multiplication table and related representations ground in situations of repeated adding their multiplicative understandings and solution procedures for the domain. Essential to the design are opportunities for students to build connections or ‘links’ between the mathematical representations and word problems depicting real-world situations. The multiplication table is a bridging tool, a pedagogical artifact designed to support students’ construction of domain-relevant situational–representational links. The apprehending-zone model draws on constructivist, social–constructivist, psychological, psycholinguistic, and philosophical resources. The model highlights the need for students to link situations and representations reciprocally into cohesive, coherent, and fluent activity structures. This model, which informed the design and evolved with it, also frames the analysis of data from implementing this design. Several learning issues, challenges inherent in some of the links students must build in this design, are identified. The dissertation presents evidence of student learning, demonstrates student variation in constructing the mathematical representations, and then tracks day-by-day interactions in one classroom implementation to show students moving from difficulty with to understanding of the identified learning issues of the design. This work contributes an innovative design for the domain of ratio and proportion as well as an original model that generalizes to other domains and may inform the practice of mathematics-education researchers as well as teachers of mathematics.
Abrahamson, D. & Cigan, C. (2003). A design for ratio and proportion. Mathematics Teaching in the Middle School, 8(9),493 – 501. Reston, Virginia: National Council of Teachers of Mathematics.
ABSTRACT: The article describes an innovative method for teaching 5th-grade students how to solve ratio and proportion word problems with understanding. The method uses the multiplication table as a conceptual support.
Abrahamson, D. (2003). Text talk, body talk, table talk: A design of ratio and proportion as classroom parallel events. In N. A. Pateman, B. J. Dougherty, & J. T. Zilliox (Eds.), Twenty Seventh Annual Meeting of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 1-8). Honolulu, Hawaii: Columbus, OH: Eric Clearinghouse for Science, Mathematics, and Environmental Education.
ABSTRACT: The paper describes the rationale and 10-day implementation in a 5th-grade classroom (n=19) of an experimental ratio-and-proportion instructional design. In this constructivist-phenomenological design, coming from our theoretical perspective, design research, and domain analysis, students: (1) link ‘real-world’ and ‘mathematical’ objects reciprocally through classroom enactment of word-problem situations vis-à-vis guided reading/writing of spatial-numeric inscriptions; (2) interpret and invent rate, ratio, and proportion texts as patterned cells in and from the multiplication table; (3) revisit and consolidate addition and multiplication as conceptual domain foundations. Students of diverse ethnicity, SES, and mathematical competence engaged successfully in discussing and solving complex problems, outperforming older students on comparison items.