STARR engages learners in a culturally situated mathematical activity involving two participants in a constructed planetarium. The dyad collaborates to navigate through the Náhookos Bi’ka’ (Big Dipper) constellation; one participant will embody the constellation’s angles and the other participant has insights into the location of the next star.
Artwork by Dongho Shin
Project team:
Rationale
Recent efforts in mathematics education aim to go beyond merely mentioning Indigenous cultural knowledge in the curriculum, instead grounding the learning in the generational cultural knowledge developed with the land (Benally et al., 2023; Eglash et al., 2006; Ruef et al., 2020). These efforts confront the exploitation of Indigenous education by Western knowledge systems; they equip the curriculum with an Indigenous perspective (Freire, 1970); and they look to the future to communialize students through the incorporation of Indigenous epistemology in education. Indigenous epistemology comes from a perceptual phenomenology of the land, as “Native science is born of a lived and storied participation with natural landscape and reality” (Cajete, 2004, p. 46). This epistemology creates an embodied ecological awareness within movement modalities (thinking, acting, interacting, etc.), an awareness that is not reflected in Western epistemology or knowledge. Western epistemology assumes a Cartesian mind-body separation, whereas Indigenous epistemology is of the natural world and of subject-subject relations (Bang, 2016). Therefore, the Indigenous epistemological perspective moves education toward new experiences through the land, classroom environment, and student interaction with objects.
Work within the embodied cognition paradigm includes embodied design– “heuristic principles for building and implementing activity genres that draw on students’ naturalistic perceptual and motor capacities” (Abrahamson, 2019, p.57). The confluence of embodied design with Indigenous epistemology suggests grounding mathematical concepts in Diné embodied epistemology, while encouraging students to experience the natural world and to find value and utility in their cultural practices. Such an approach focuses on creating resources for Indigenous students to restructure (Wilensky & Papert, 2010) mathematics in the intersections of Indigenous mathematics and Western mathematics. The STARR project utilizes cultural–historical forms of astrometrical perception and creates opportunities for the student to reinstate Diné sensorimotor phenomenology of an angle as egocentric dynamical enactment, thus favoring realistic sensorimotor experience over formal symbolic computation. In particular, STARR affords students the opportunity to perform qualitative and quantitative mathematical processes in a learning environment that simulates essential perspectival qualities of Diné archaeoastronomical practice, in dialogic negotiation with Euclidean geometry (Benally et al., 2023), thus creating an epistemologically pluralistic learning environment (Turkle & Papert, 1991). In the anthropology of space, Pinxten et al., (1983) first introduced a semantic analysis of the Navajo language around space, created with community members, which provides the basis for a Diné mathematics education evolution. This evolution and development of pedagogy largely depends on the Indigenous language, as languages hold important perspectival qualities and exhibit the peoples relationship to the land: “Prepositions, adjectivals, adverbials, nouns and verbal structures associated with position are all possible ways of referring to space, but it may be more complicated by the way in which words are positioned in different languages” (Owens, 2013, p. 954). The Diné oral language is action-based, so that the created mathematical discourse and “geometrical reference is carried in the verb, rather than the noun” (Barton, 2008, p.29). The language structures “represent the geography, ecology and cultural significance of spaces as places” (Ownes, 2013, p.954). Indigenous languages bring pedagogical promise to mathematics education by bringing to light alternative ways of mathematically orienting to the environment (Barton, 2008).
Design
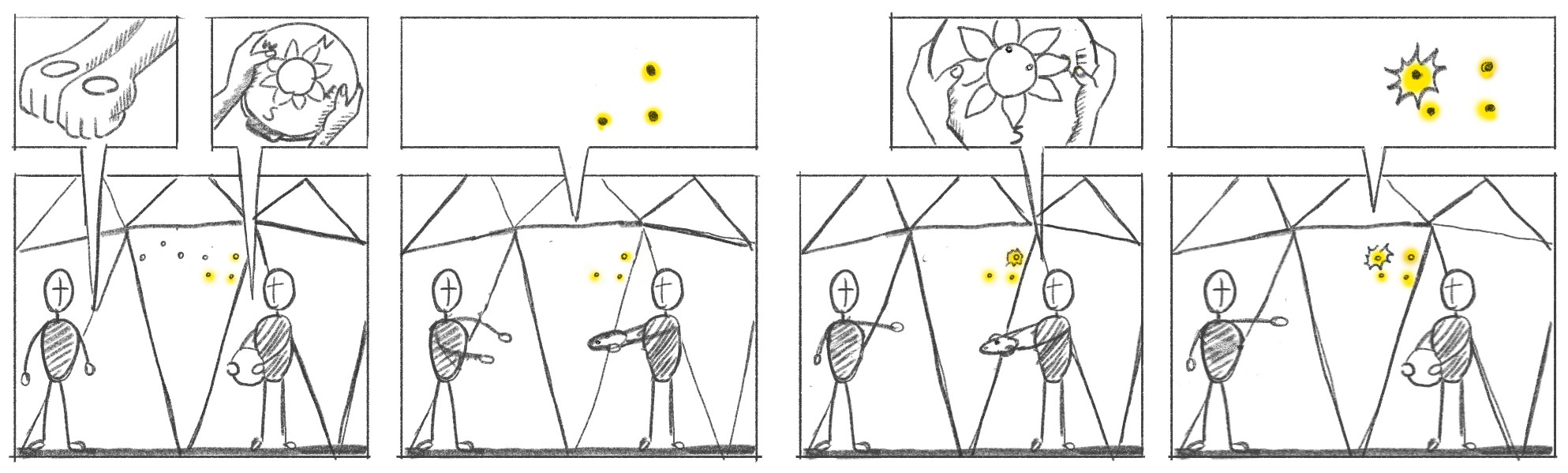
Figure 2. STARR components: (a) Planetarium; (b) LED constellation; (c) hand-held compass; (d) Octagon rug; and (e) Mugic glove sensors.
The STARR installation —Students Tracking Angular Rotation Recorder—is a tangible cultural interface designed for young students to learn the basic geometry content of angles by experiencing angular rotation from multiple complementary perspectives. The design features a 5.5’ x 5.5’ x 5.5’ nylon-covered tent as the planetarium, constructed from dowels and plastic tubing (Figure 2a). The planetarium ceiling bears LED displays shaped after the Náhookos Bi’ka’ (Big Dipper) as it is oriented during the fall season (Figure 2b), above which lies the Náhookos Biko’ (North Star). Lying in the center of the planetarium is an octogonal cotton rug with a clear plastic center featuring a compass rose (Figure 2d). The octagon was designed to prompt participants’ visual attention toward the planetarium’s eight unique spatial orientations (cardinal directions). One participant has the Magic sensor gloves on (Figure 2e) and the other participant holds an embroidery hoop with a compass rose design and 24 LED circles which track the movement of the sensors (Figure 2c). Participating pairs metaphorically traverse along the constellation; the sensor iteratively connects to the past star, situating herself in the current star, and orienting to the next star.
The constellations Náhookos Bi’ka’ (Male Revolving One) and Náhookos Biko’ (Central Fire) make up two of three parts of the Náhookos constellation, the other being Náhookos Bi’áád (Female Revolving One), which continually revolve around Náhookos Biko’. This positioning is grounded in and from the Diné homeland, Diné Bikéyah; “Navajos have organized their star knowledge from Diné Bikéyah, a central location in the American southwest defined by the four sacred mountains. The order of the Navajo constellations is related to the geographical information provided from the cardinal directions, which, in turn, are directly connected to cosmic stellar processes as observed from this position of centrality in Diné Bikéyah” (Maryboy & Begay, 2005, p. 14-15). The task of finding or constructing the constellations grew from the Diné story of how the stars came to be (retold in Oughton, 1992 by Hosteen Klah). In this story, the stars lie in chaos because of the actions of Coyote. Therefore, the participants must make sense of the sky by identifying one of these important constellations.
Activity
The STARR learning environment is built in the form of a small planetarium to invoke an experience of the night sky. Figure 3 shows two students in the planetarium, engaged in the task of traversing the night sky by indicating stars using different media. The student on the left is the “Sensor” who virtually becomes each new star of the constellation (1st-person perspective); the student on the right is the “Navigator” who guides the “Sensor” (via 3rd-person perspective on the same constellation). The Sensor must use their left arm as a ray to connect the past star to the current star that they embody, and their right arm as a ray to discover the next star in the constellation. The Navigator aids the Sensor by providing feedback from the compass, which tracks the location of the second (right arm) sensor. This initiates dialogue in the service of finding the exact location of the next star. This is an iterative process where the Sensor, again, becomes the most recent star found, and they again connect to the past star and the next star.
There are several different ways that one can construe an angle. STARR focuses the participants on the angle’s ‘open-ness’ (i.e., the rotated aperture between the angle’s two arms), where participants determine the angle’s magnitude “by measuring the length of the arc <the interior> that the angle subtends in a circle centered at the angle’s vertex” (Hardison, 2019, p. 35).
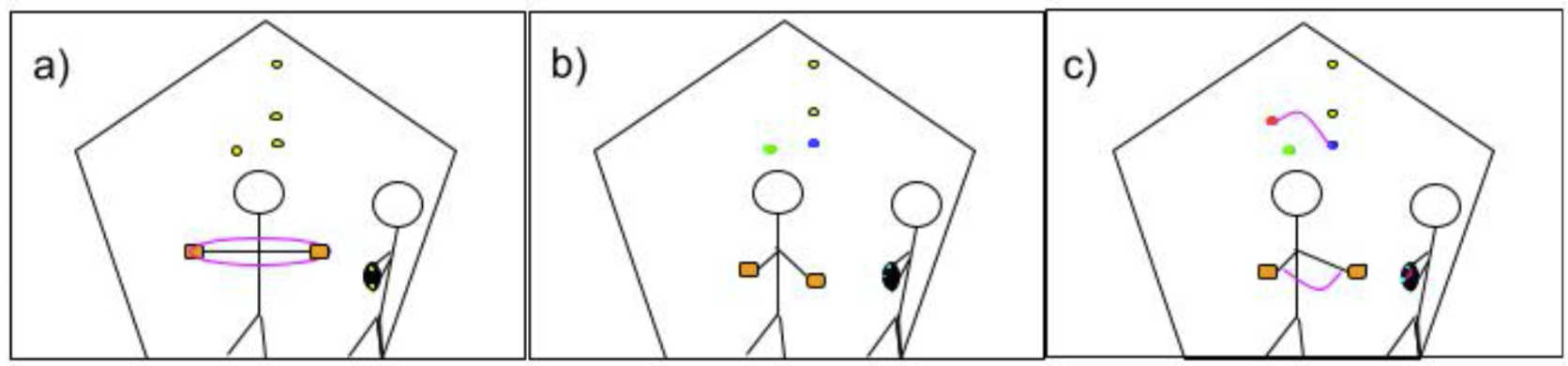Figure 3: (a) Two students inside the planetarium playing, one with the hand sensors (orange rectangles), the other holding the embroidery compass (black circle). (b) The Sensor is metaphorically the current star (shown as the green dot); and is connected to the past star (blue dot) and is finding the next star; (c) Having built the star connection by finding the next star (red dot), the pink lines depict the angular rotation of both the student and the stars, as indicated on the compass.
The Sensor points one arm and exploratorily moves it in the plane parallel to the ground (Figure 3a), searching for the next star. In Figure 3b the Sensor is on the third star of Náhookos Bi’ka’; here, one arm is connected to the past star, and they are looking for the connection to the next star. The Navigator sees the compass color coding, providing vital supplementary information to guide the Sensor. The Navigator communicates the Sensor’s rotation. In Figure 3c, they have found the correct location of the next star and have completed the current angle (e.g. the pink lines). In the next iteration, the Sensor then embodies the star most recently lit.
Publications
Benally, J. (2024, June 17–20). Co-constructing N´ahookos Bi’ka’ constellation with STARR <Doctoral Consortium>. In J. P. Hourcade & H. M. Skovbjerg (Eds.), ”Inclusive Happiness” – Proceedings of the 23rd Annual ACM Interaction Design and Children Conference, Delft, Netherlands. Association for Computing Machinery, ACM, New York, NY, USA. https://doi.org/10.1145/3628516.3659861
Benally, J. (2024, June 17–20). Co-constructing N´ahookos Bi’ka’ constellation with STARR <Demo>. In E. M. Bonsignore & M. Horton (Eds.), ”Inclusive Happiness” – Proceedings of the 23rd Annual ACM Interaction Design and Children Conference, Delft, Netherlands. Association for Computing Machinery, ACM, New York, NY, USA. https://doi.org/10.1145/3628516.3661161
Benally, J. (2024, April). Angling the stars: A Geometry Design Reconciling Indigenous and Colonial Perceptions. In D. Abrahamson (Chair) & S. Gerofsky (Discussant), In-sight out: Challenges and opportunities in learning mathematics through negotiating egocentric and allocentric perspectives. Symposium presented for the SIG Research in Mathematics Education at the annual meeting of the American Educational Research Association, Philadelphia, April 11–14.
Benally, J., Palatnik, A., Ryokai, K., & Abrahamson, D. (2022). Learning through negotiating conceptually generative perspectival complementarities: The case of geometry. For the Learning of Mathematics, 42(3), 34–41.
Benally, J. (2020, Mar). Dynamic embodied angles in a simulated restorative planetarium. Poster accepted for presentation at the annual Research Day, Graduate School of Education, University of California, Berkeley.